
Why Does A Tyre Grip The Road? Part 3 - Longitudinal Grip
This is part 3 of our Why Does A Tyre Grip The Road series, today we will be looking into Longitudinal grip. The first post covered rubber and the second looked at grip more generally, you don’t need to read them to understand this one, but it will help to provide a bit more colour, read the first one here and the second one here.
Grip
Grip depends on a number of things, but it can be summed up simply, but not completely accurately in the following equation
Where X = Friction Force
μ = Coefficient of friction (CoF)
Z = Vertical load on the tyre
This equation hides just how complicated grip is, just two variables, one related to the weight of the vehicle, the other to the tyre and road interface. But when we think about it a little more, we can see that even the simpler to understand variable, Z, is loaded. Weight shifts, it’s transferred around the car during acceleration, braking, and cornering. Therefore the load experienced at each tyre is ever changing, there is no one load on a tyre, there is no one level of grip for a tyre. Multiply this by four and things really start to get complicated. And then we think a little about the other variable, the coefficient of friction (CoF), which is simply the amount of force needed to slide a tyre along a surface divided by the weight of the tyre (Normal force), fairly simple stuff. It’s what's hidden inside the CoF that makes this so interesting. It changes along with anyone of the following, tyre pressure, track temp, ambient temp, tyre temp, roughness of the road, wetness of the road, tyre compound, tyre wear, tread pattern, tyre cleanliness, road cleanliness, contact patch size, vehicle speed, and no doubt many other things that I have forgotten to write, but the main takeaway is that it's affected by a large number of variables, making this stuff super interesting.
Before we get too deep in the weeds, an interesting thing about the above equation is that as the load on the vehicle increases the friction force also increases, but despite appearances, the increase isn’t linear. CoF is negatively affected by vertical load, as the load increases, the CoF decreases. But any decreases in friction from the lower CoF are dwarfed by increasing vertical load’s effect on friction; if this wasn’t the case aero wouldn’t work. We can see both of these effects in the graphs below, on the left we can see the decrease in CoF from the increasing vertical load and on the right, the increasing longitudinal grip force for a range of vertical loads. As the vertical load is increased from roughly 1500N (152kg) to 6000N (612kg) the CoF reduces from 1.2 to roughly 0.95. Despite this, we can see on the right that the longitudinal frictional force increases with higher vertical loads, more vertical load means more grip.

Longitudinal Grip
Grip in the longitudinal (forward and backwards) direction is governed by the slip ratio, which is the difference between the wheel speed and the vehicle’s speed. As a car is travelling along, the wheels and vehicle all travel at the same speed, however, when the brakes are applied the wheel speed is slowed down relative to the vehicle’s speed. This causes the tyre’s rubber at the contact patch to shear and slip, creating grip, see the second post in the series for more on this. As slip is needed to create grip, the greater the slip ratio, the greater the grip, but only up to a point, more on this later. The slip ratio is expressed as a percentage between -1 (wheel locked) and +∞ (wheel spinning) and can be expressed mathematically as

where G = Slippage rate
⍵ = Angular speed of the wheel,
R = Rolling radius, combined (⍵R) they are the rolling speed of the tyre, and
V = Vehicle’s speed
If we zoom in on where a tyre touches the ground, we can see what's going on when we apply the brakes a little more clearly. As new sections of the contact patch touch down, the first two blocks on the right in the image below, the rubber initially deforms under the weight of the car. As the blocks continue to make their way towards the back of the vehicle, the rubber begins to experience two opposing forces, slippage where the rubber attaches to the belt and grip where the rubber meets the ground. Initially the grip force is able to match the slippage force, causing the block to only shear. But as the block travels further rearward and the slippage force increases, eventually we reach the point where grip is unable to continue to hold on, the block is now slipping.

We can therefore make two phases within a contact patch, the shear and the slippage phases. The percentage of each is a key component in the amount of grip a tyre is able to generate. If we graph the slip ratio against the CoF, we can see that increasing the slip ratio increases the CoF to its maximum (μmax), after which our grip deteriorates.

Michelin states that for a road tyre μmax is reached around 10% of slippage, but for a race tyre, because there is little to no tread, max friction is generated around 2 - 3% of slippage.
The cause for this grip deterioration is increasing tyre temperatures. As slip is increased and the rubber continues to heat up, eventually it will begin to negatively affect the CoF, it will begin to enter the downward phase of the next graph. As the CoF decreases, we have less friction force, this if left unchecked will result in a runaway situation, the tyres heat up more, the CoF reduces, slip is increased, the tyres heat up more, the CoF reduces, slip is increased, with the cycle continuing until the the tyres lock up, and we end up in the barrier or bushes.

The loss of friction at higher temps, as stated in the first article, is because as the rubber transitions towards its rubbery state, the polymer strands are creating less internal friction and therefore less hysteresis, less grip.

An interesting outcome of the temperature curve is that we can achieve a level of friction from two different temperatures. This means, depending on whether we have travelled past the peak CoF or not, despite the fact that we have the same level of grip, the tyre temperatures will be vastly different, see below.

Temperatures Impact
We know that how we drive impacts the tyre temperature, but what about things that we don’t have control over, the pavement temp (PT), the atmospheric temp (AT), and the Contained air temp (CAT - Temp within tyre)? Lucky for us Anupam, K. 2021 [5] has modelled these against the CoF on a porous asphalt (PA). As you have probably suspected, an increase in any of these increases the tyre temp and therefore decreases the CoF. Pavement temperature had the biggest impact, atmospheric was second, with the contained air temperature having very little effect. I was surprised by the fact that the contained air temperature had such a small effect, so I did some maths. It turns out that an increase of 10℃ in the tyre air temp only increases tyre pressure by 0.56psi, nowhere near as much as I had thought, and wouldn’t deform the tyre enough to impact the contact patch. That temperature would also need to make its way through a large amount of layers before it got to the rubber and no doubt used up most of it travelling.

Using the ideal gas law we can get a fairly close answer fairly simply. 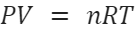
Where P = Pressure
V = Volume
n = Number of moles or the amount of gas
R = Ideal gas constant
T = Temperature
Assumptions
1. Air is being used to fill the tyres
2. Air is a ideal gas
3. Our gauge pressure is 32psi, so our absolute pressure is 32-14.7 = 17.3psi or 119279.3 Pascals
4. Volume - The figure I used was from this quora question, not a race tyre but should get us a good idea of the change without me having to do extra work. They get a volume figure of 0.03576m3
5. n we need to calculate
6. R is 8.314 J/mol K
7. T = AT + 10℃ and AT + 20℃ with AT being 20℃, so our temps in Kelvin are 303.15K and 313.15K
First we need to calculate the n for our first case, with a little rearranging we get

And when we plug in the values
Now we have the number of moles, we can calculate the change in pressure.
Again if we rearrange the ideal gas law equation we get
Add that back to the atmospheric pressure and we have a new gauge pressure of just 32.56psi, an increase of just 0.56psi.
We can double check this with some even simpler maths. For an enclosure the temperature and pressure are directly related, we can therefore say that if we know the pressure and temperature at one setting and one of the two at another, we can calculate the missing value. For our example, we know pressure and temperature at 30℃ and we want to know pressure at 40℃, so using this info and the equation below, we can work out the pressure at 40℃. Again we need to convert these figures to absolute temp and pressure for this to work.
I would say that’s close enough for a check on a rough calculation, but if you see a mistake let me know, I’m always keen to learn.
Speeds impact
Temperatures aren’t the only things affecting grip levels, speed does as well. It, similar to temperature, reduces grip as it is increased. The top graph below shows the effect increasing speeds will have on friction with a slip ratio of 15% and the one below it is at a slip ratio of 100%. The data that we are most interested in is the PA (Porous Asphalt) line as this most resembles tarmac that we will see.

Loads impact


Unfortunately this brings us to the end of another post, but never fear, we have other great posts already up for you to enjoy and will continue to post into the future. Next we will be looking into lateral grip, the link for it is below, but if you want to check out something else tyre related, see the links to this series below. Don’t forget to sign up so you don’t miss an article and as always, if you have any comments, suggestions, or noticed I made a mistake, either write it down in the comments or get in contact via email or using the contact page, I’d love to hear it. Thanks for reading and I hope you have a great day.
Why Does A Tyre Grip The Road Series
References:
[1] jc50d, 2017, 'summernats 17 Gary Myers burnout', Link[2] Li, L. 2014, ‘Comprehensive tire–road friction coefficient estimation based on signal fusion method under complex maneuvering operations’, Link, retrieved on 11/03/22
[3] Michelin, The Tyre Grip, Link, retrieved on 03/03/22
[4] Balkwill, J. 2017, 'Performance Vehicle Dynamics'
[5] Anupam, K. 2021, 3-D Thermomechanical Tire–Pavement Interaction Model for Evaluation of Pavement Skid Resistance, Link, retrieved on 11/03/22
[6] Behroozinia, P. 2018, 'An investigation towards intelligent tyres using finite element analysis', Link, retrieved 5/04/22




No comments:
Post a Comment